原文链接，转载请注明出处

2.20

$$\text{AUC}=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1} - x_i)\cdot(y_i + y_{i+1})$$ [解析]：在解释$\text{AUC}$公式之前，我们需要先弄清楚$\text{ROC}$曲线的具体绘制过程，下面我们就举个例子，按照西瓜书图2.4下方给出的绘制方法来讲解一下$\text{ROC}$曲线的具体绘制过程。假设我们已经训练得到一个学习器$f(s)$，现在用该学习器来对我们的8个测试样本（4个正例，4个反例，也即$m^+=m^-=4$）进行预测，假设预测结果为： $$(s_1,0.77,+),(s_2,0.62,-),(s_3,0.58,+),(s_4,0.47,+)$$ $$(s_5,0.47,-),(s_6,0.33,-),(s_7,0.23,+),(s_8,0.15,-)$$ 其中，$+$和$-$分别表示为正例和为反例，里面的数字表示学习器$f(s)$预测该样本为正例的概率，例如对于反例$s_2$来说，当前学习器$f(s)$预测它是正例的概率为$0.62$。根据西瓜书上给出的绘制方法可知，首先需要对所有测试样本按照学习器给出的预测结果进行排序（上面给出的预测结果已经按照预测值从大到小排好），接着将分类阈值设为一个不可能取到的最大值，显然这时候所有样本预测为正例的概率都一定小于分类阈值，那么预测为正例的样本个数为0，相应的真正例率和假正例率也都为0，所以此时我们可以在坐标$(0,0)$处打一个点。接下来我们需要把分类阈值从大到小依次设为每个样本的预测值，也就是依次设为$0.77、0.62、0.58、0.47、0.33、0.23、0.15$，然后每次计算真正例率和假正例率，再在相应的坐标上打一个点，最后再将各个点用直线串连起来即可得到$\text{ROC}$曲线。需要注意的是，在统计预测结果时，预测值等于分类阈值的样本也算作预测为正例。例如，当分类阈值为$0.77$时，测试样本$s_1$被预测为正例，由于它的真实标记也是正例，所以此时$s_1$是一个真正例。为了便于绘图，我们将$x$轴（假正例率轴）的“步长”定为$\frac{1}{m^-}$，$y$轴（真正例率轴）的“步长”定为$\frac{1}{m^+}$，这样的话，根据真正例率和假正例率的定义可知，每次变动分类阈值时，若新增$i$个假正例，那么相应的$x$轴坐标也就增加$\frac{i}{m^-}$，同理，若新增$j$个真正例，那么相应的$y$轴坐标也就增加$\frac{j}{m^+}$。按照以上讲述的绘制流程，最终我们可以绘制出如下图所示的$\text{ROC}$曲线

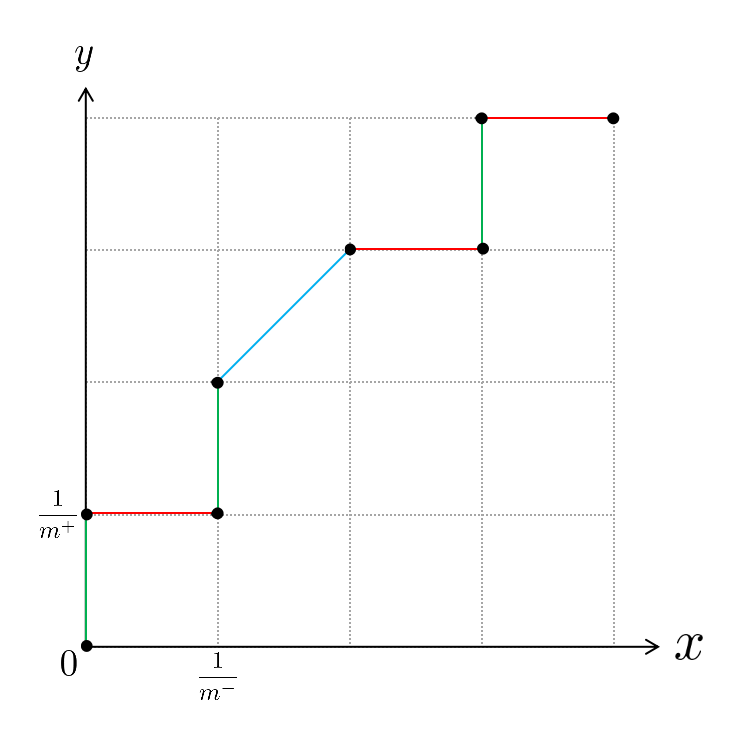
2.21

$$\ell_{rank}=\frac{1}{m^+m^-}\sum_{\boldsymbol{x}^+ \in D^+}\sum_{\boldsymbol{x}^- \in D^-}\left(\mathbb{I}\left(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)\right)+\frac{1}{2}\mathbb{I}\left(f(\boldsymbol{x}^+)=f(\boldsymbol{x}^-)\right)\right)$$ [解析]：按照我们上述对公式(2.20)的解析思路，$\ell_{rank}$可以看作是所有绿色线段和蓝色线段与$y$轴围成的面积之和，但是公式(2.21)很难一眼看出其面积的具体计算方式，因此我们需要将公式(2.21)进行恒等变形 $$\begin{aligned} \ell_{rank}&=\frac{1}{m^+m^-}\sum_{\boldsymbol{x}^+ \in D^+}\sum_{\boldsymbol{x}^- \in D^-}\left(\mathbb{I}\left(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)\right)+\frac{1}{2}\mathbb{I}\left(f(\boldsymbol{x}^+)=f(\boldsymbol{x}^-)\right)\right) \\ &=\frac{1}{m^+m^-}\sum_{\boldsymbol{x}^+ \in D^+}\left[\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)\right)+\frac{1}{2}\cdot\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)=f(\boldsymbol{x}^-)\right)\right] \\ &=\sum_{\boldsymbol{x}^+ \in D^+}\left[\frac{1}{m^+}\cdot\frac{1}{m^-}\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)\right)+\frac{1}{2}\cdot\frac{1}{m^+}\cdot\frac{1}{m^-}\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)=f(\boldsymbol{x}^-)\right)\right] \\ &=\sum_{\boldsymbol{x}^+ \in D^+}\frac{1}{2}\cdot\frac{1}{m^+}\cdot\left[\frac{2}{m^-}\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)\right)+\frac{1}{m^-}\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)=f(\boldsymbol{x}^-)\right)\right] \\ \end{aligned}$$ 根据公式(2.20)中给出的$\text{ROC}$曲线图可知，在变动分类阈值的过程当中，如果有新增真正例，那么相应地就会增加一条绿色线段或蓝色线段，所以上式中的$\sum\limits_{\boldsymbol{x}^+ \in D^+}$可以看作是在遍历所有绿色和蓝色线段，那么相应地$\sum\limits_{\boldsymbol{x}^+ \in D^+}$后面的那一项便是在求绿色线段或者蓝色线段与$y$轴围成的面积，也即 $$\frac{1}{2}\cdot\frac{1}{m^+}\cdot\left[\frac{2}{m^-}\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)\right)+\frac{1}{m^-}\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)=f(\boldsymbol{x}^-)\right)\right]$$ 同公式(2.20)中的求解思路一样，不论是绿色线段还是蓝色线段，其与$y$轴围成的图形面积都可以用梯形公式来进行计算，所以上式表示的依旧是一个梯形的面积求解公式。其中$\frac{1}{m^+}$即为梯形的“高”，中括号中的那一项便是“上底+下底”，下面我们来分别推导一下“上底”（较短的那个底）和“下底”。由于在绘制$\text{ROC}$曲线的过程中，每新增一个假正例时$x$坐标也就新增一个单位，所以对于“上底”，也就是绿色或者蓝色线段的下端点到$y$轴的距离，它就等于$\frac{1}{m^-}$乘以预测值比$\boldsymbol{x^+}$大的假正例的个数，也即 $$\frac{1}{m^-}\sum\limits_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)\right)$$ 而对于“下底”，它就等于$\frac{1}{m^-}$乘以预测值大于等于$\boldsymbol{x^+}$的假正例的个数，也即 $$\frac{1}{m^-}\left(\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)\right)+\sum_{\boldsymbol{x}^- \in D^-}\mathbb{I}\left(f(\boldsymbol{x}^+)=f(\boldsymbol{x}^-)\right)\right)$$

2.27

$$\overline{\epsilon}=\max \epsilon\quad \text { s.t. } \sum_{i= \epsilon_{0} \times m+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) \epsilon^{i}(1-\epsilon)^{m-i}<\alpha$$

[推导]：截至2018年12月，第一版第30次印刷，公式（2.27）应当勘误修正为 $$\overline{\epsilon}=\min \epsilon\quad\text { s.t. } \sum_{i=\epsilon\times m+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) \epsilon_0^{i}(1-\epsilon_0)^{m-i}<\alpha$$ 具体推导过程如下：由西瓜书中的上下文可知，对$\epsilon\leq\epsilon_0$进行假设检验，等价于附录①中所述的对$p\leq p_0$进行假设检验，所以在西瓜书中求解最大错误率$\overline{\epsilon}$等价于在附录①中求解事件最大发生频率$\frac{\overline{C}}{m}$。由附录①可知 $$\overline{C}=\min C\quad\text { s.t. } \sum_{i=C+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) p_0^{i}(1-p_0)^{m-i}<\alpha$$ 所以 $$\frac{\overline{C}}{m}=\min \frac{C}{m}\quad\text { s.t. } \sum_{i=C+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) p_0^{i}(1-p_0)^{m-i}<\alpha$$ 将上式中的$\frac{\overline{C}}{m},\frac{C}{m},p_0$等价替换为$\overline{\epsilon},\epsilon,\epsilon_0$可得 $$\overline{\epsilon}=\min \epsilon\quad\text { s.t. } \sum_{i=\epsilon\times m+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) \epsilon_0^{i}(1-\epsilon_0)^{m-i}<\alpha$$

2.41

$$\begin{aligned} E(f ; D)=& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})+\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ &+\mathbb{E}_{D}\left[+2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y+y-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y\right)^{2}\right]+\mathbb{E}_{D}\left[\left(y-y_{D}\right)^{2}\right]\\ &+2 \mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y\right)\left(y-y_{D}\right)\right]\\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\left(\bar{f}(\boldsymbol{x})-y\right)^{2}+\mathbb{E}_{D}\left[\left(y_{D}-y\right)^{2}\right] \end{aligned}$$

[解析]：

• 第1-2步：减一个$\bar{f}(\boldsymbol{x})$再加一个$\bar{f}(\boldsymbol{x})$，属于简单的恒等变形；
• 第2-3步：首先将中括号里面的式子展开 $$\mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}+\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}+2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right]$$ 然后根据期望的运算性质：$\mathbb{E}[X+Y]=\mathbb{E}[X]+\mathbb{E}[Y]$可将上式化为 $$ \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] +\mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right]$$
• 第3-4步：再次利用期望的运算性质将第3步得到的式子的最后一项展开 $$\mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] = \mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot\bar{f}(\boldsymbol{x})\right] - \mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot y_{D}\right]$$
  • 首先计算展开后得到的第一项 $$\mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot\bar{f}(\boldsymbol{x})\right] = \mathbb{E}_{D}\left[2f(\boldsymbol{x} ; D)\cdot\bar{f}(\boldsymbol{x})-2\bar{f}(\boldsymbol{x})\cdot\bar{f}(\boldsymbol{x})\right]$$ 由于$\bar{f}(\boldsymbol{x})$是常量，所以由期望的运算性质：$\mathbb{E}[AX+B]=A\mathbb{E}[X]+B$（其中$A,B$均为常量）可得 $$\mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot\bar{f}(\boldsymbol{x})\right] = 2\bar{f}(\boldsymbol{x})\cdot\mathbb{E}_{D}\left[f(\boldsymbol{x} ; D)\right]-2\bar{f}(\boldsymbol{x})\cdot\bar{f}(\boldsymbol{x})$$ 由公式（2.37）可知：$\mathbb{E}_{D}\left[f(\boldsymbol{x} ; D)\right]=\bar{f}(\boldsymbol{x})$，所以 $$\mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot\bar{f}(\boldsymbol{x})\right] = 2\bar{f}(\boldsymbol{x})\cdot\bar{f}(\boldsymbol{x})-2\bar{f}(\boldsymbol{x})\cdot\bar{f}(\boldsymbol{x})=0$$
  • 接着计算展开后得到的第二项 $$\mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot y_{D}\right]=2\mathbb{E}_{D}\left[f(\boldsymbol{x} ; D)\cdot y_{D}\right]-2\bar{f}(\boldsymbol{x})\cdot \mathbb{E}_{D}\left[y_{D}\right]$$ 由于噪声和$f$无关，所以$f(\boldsymbol{x} ; D)$和$y_D$是两个相互独立的随机变量，所以根据期望的运算性质：$\mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]$（其中$X$和$Y$为相互独立的随机变量）可得 $$\begin{aligned} \mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot y_{D}\right]&=2\mathbb{E}_{D}\left[f(\boldsymbol{x} ; D)\cdot y_{D}\right]-2\bar{f}(\boldsymbol{x})\cdot \mathbb{E}_{D}\left[y_{D}\right] \\ &=2\mathbb{E}_{D}\left[f(\boldsymbol{x} ; D)\right]\cdot \mathbb{E}_{D}\left[y_{D}\right]-2\bar{f}(\boldsymbol{x})\cdot \mathbb{E}_{D}\left[y_{D}\right] \\ &=2\bar{f}(\boldsymbol{x})\cdot \mathbb{E}_{D}\left[y_{D}\right]-2\bar{f}(\boldsymbol{x})\cdot \mathbb{E}_{D}\left[y_{D}\right] \\ &= 0 \end{aligned}$$ 所以 $$\begin{aligned} \mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] &= \mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot\bar{f}(\boldsymbol{x})\right] - \mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\cdot y_{D}\right] \\ &= 0+0 \\ &=0 \end{aligned}$$
• 第4-5步：同第1-2步一样，减一个$y$再加一个$y$，属于简单的恒等变形；
• 第5-6步：同第2-3步一样，将最后一项利用期望的运算性质进行展开；
• 第6-7步：因为$\bar{f}(\boldsymbol{x})$和$y$均为常量，所以根据期望的运算性质可知，第6步中的第2项可化为 $$\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y\right)^{2}\right]=\left(\bar{f}(\boldsymbol{x})-y\right)^{2}$$ 同理，第6步中的最后一项可化为 $$2\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y\right)\left(y-y_{D}\right)\right]=2\left(\bar{f}(\boldsymbol{x})-y\right)\mathbb{E}_{D}\left[\left(y-y_{D}\right)\right]$$ 由于此时假设噪声的期望为零，也即$\mathbb{E}_{D}\left[\left(y-y_{D}\right)\right]=0$，所以 $$2\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y\right)\left(y-y_{D}\right)\right]=2\left(\bar{f}(\boldsymbol{x})-y\right)\cdot 0=0$$

附录

①二项分布参数$p$的检验^[1]

设某事件发生的概率为$p$，$p$未知，作$m$次独立试验，每次观察该事件是否发生，以$X$记该事件发生的次数，则$X$服从二项分布$B(m,p)$，现根据$X$检验如下假设： $$\begin{aligned} H_0:p\leq p_0\\ H_1:p > p_0 \end{aligned}$$ 由二项分布本身的特性可知：$p$越小，$X$取到较小值的概率越大。因此，对于上述假设，一个直观上合理的检验为 $$\varphi:\text{当}X\leq C\text{时接受}H_0,\text{否则就拒绝}H_0$$ 其中，$C\in N$表示事件最大发生次数。此检验对应的功效函数为 $$\begin{aligned} \beta_{\varphi}(p)&=P(X>C)\\ &=1-P(X\leq C) \\ &=1-\sum_{i=0}^{C}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) p^{i} (1-p)^{m-i} \\ &=\sum_{i=C+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) p^{i} (1-p)^{m-i} \\ \end{aligned}$$ 由于“$p$越小，$X$取到较小值的概率越大”可以等价表示为：$P(X\leq C)$是关于$p$的减函数（更为严格的数学证明参见参考文献[1]中第二章习题7），所以$\beta_{\varphi}(p)=P(X>C)=1-P(X\leq C)$是关于$p$的增函数，那么当$p\leq p_0$时，$\beta_{\varphi}(p_0)$即为$\beta_{\varphi}(p)$的上确界。又因为，根据参考文献[1]中5.1.3的定义1.2可知，检验水平$\alpha$默认取最小可能的水平，所以在给定检验水平$\alpha$时，可以通过如下方程解得满足检验水平$\alpha$的整数$C$： $$\alpha =\sup \left\{\beta_{\varphi}(p)\right\}$$ 显然，当$p\leq p_0$时： $$\begin{aligned} \alpha &=\sup \left\{\beta_{\varphi}(p)\right\} \\ &=\beta_{\varphi}(p_0) \\ &=\sum_{i=C+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) p_0^{i} (1-p_0)^{m-i} \end{aligned}$$ 对于此方程，通常不一定正好解得一个整数$C$使得方程成立，较常见的情况是存在这样一个$\overline{C}$使得 $$\begin{aligned} \sum_{i=\overline{C}+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) p_0^{i} (1-p_0)^{m-i}<\alpha \\ \sum_{i=\overline{C}}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) p_0^{i} (1-p_0)^{m-i}>\alpha \end{aligned}$$ 此时，$C$只能取$\overline{C}$或者$\overline{C}+1$，若$C$取$\overline{C}$，则相当于升高了检验水平$\alpha$，若$C$取$\overline{C}+1$则相当于降低了检验水平$\alpha$，具体如何取舍需要结合实际情况，但是通常为了减小犯第一类错误的概率，会倾向于令$C$取$\overline{C}+1$。下面考虑如何求解$\overline{C}$：易证$\beta_{\varphi}(p_0)$是关于$C$的减函数，所以再结合上述关于$\overline{C}$的两个不等式易推得 $$\overline{C}=\min C\quad\text { s.t. } \sum_{i=C+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) p_0^{i}(1-p_0)^{m-i}<\alpha$$

参考文献

[1]陈希孺编著.概率论与数理统计[M].中国科学技术大学出版社,2009.